By Sanjay Joshi and Richard Ross. ICP testing has become more mainstream in the past few years since it was introduced in the hobby almost a decade ago, but questions about the utility of the testing results remain.
ICP testing provides a relatively affordable service simultaneously testing the concentration of many major and minor trace elements in salt water. Several reefkeeping methodologies have been developed to manage and adjust individual elements based on ICP test results. Fundamental to these methodologies is the assumption that the ICP testing and results are accurate and repeatable – but is that assumption a correct assumption?
- How accurate and repeatable are reef hobby ICP test results?
- What is the level of uncertainty associated with the measurements?
- Are there significant differences between the results from different ICP vendors?
This article hopes to help shed more light on the repeatability of the ICP tests, the level of uncertainty in the measurements, and whether there are statistically significant differences between the results from different vendors.
Determining the accuracy of tests requires that the tests be performed on a known sample called a certified reference standard and then comparing the known composition with the measurement results. The high cost of existing certified reference standards has made it difficult to really determine the accuracy of hobby ICP testing both from test to test from the same vendor, and across different vendors (though there has been some effort to do this) [1].
There have been several attempts to address these issues. Some have tried to address this issue by using double-blind samples of two water samples being sent to a testing vendor – one with the normal water from an aquarium and another with the same water being spiked with known quantities of elements and evaluating the accuracy of these tests based on the ability to detect the correct amount of spiked element added [2].
Recently, Sanjay Joshi [3] showed the results of testing the same water sample by 5 different ICP vendors to show the differences from vendor to vendor. However, while the results showed visible differences, they were based on just one sample each and hence not statistically quantifiable.
This paper focuses on addressing the repeatability (or precision) of the ICP tests by using several test samples of the same water sent to 3 ICP-testing vendors and using statistical measures to quantify the repeatability by evaluating the observed variability. Assessments can be made based on this variability as to whether the differences between the tests are statistically significant or just a result of measurement noise.
The intent here is not to single out specific vendors, but to share with the reef community the methodology of our analysis and conclusions on addressing the questions – How repeatable are the results? Are there statistically significant differences in the results between different vendors? Can we get some sense of the uncertainty associated with the measurements? For this work, we are ignoring the question of overall accuracy, instead, we are trying to determine how practical, repeatable, and actionable the results of the same test water are, both from a single vendor and across 3 vendors.
Method
Five tests were acquired from three different ICP vendors with five replicate water samples sent to each vendor. These replicates allow for understanding the variability that may be present in the testing. The vendors were chosen arbitrarily, based on test kit availability, and three vendors were used because the costs of reef hobby ICP testing at this scale are not insignificant, and we felt three vendors were enough to get at the questions we are interested in addressing.
As with any experiment, the more replicates measured, the more the spread in the results will reflect the true precision of ICP testing, however, the added cost is always a consideration. The tests used in this project were purchased for our use by the Reef Beef Podcast [4] – and we thank all those involved with that decision.
Roughly 3 gallons of water were drawn from an aquarium and placed in a container for distribution to the testing vendors. 15 samples were collected for testing within the span of time it took to fill all the sample tubes with water. The samples were shipped arbitrarily, five at a time, on Monday, Wednesday, and Friday of the same week. The samples were submitted anonymously so as not to bias the results in any way. For the experiment, given the limited number of vendors used, we have decided to keep the vendors anonymous.
Results
The results are presented in two sections. The first section presents the results from each vendor and the analysis of the repeatability of the results. The second section compares the results across the vendors to evaluate the differences across the vendors. To maintain the anonymity of the vendors, the results are only reported here for the elements common to all the tests. The elements are ordered based on decreasing concentrations. All concentrations were converted to mg/L for the sake of consistency.
1. Repeatability of the ICP Tests
The repeatability of tests refers to the consistency or reliability of the results when the same test is conducted multiple times on the same sample. In other words, if you were to perform a test or measurement repeatedly, how closely would the results match each time? High repeatability implies that the test produces consistent results with low variability around the mean value.
Repeatability is a measure of precision. A test is considered precise if repeated measurements produce results with low variability around the mean. Various factors can affect repeatability, such as sample matrix (in this case, seawater or artificial seawater) equipment calibration, skill of the operators, environmental conditions, signal-to-noise ratio of the instrument, and more. Repeatability is assessed using statistical measures such as standard deviation (SD) which supplies information on how dispersed the data are around the mean.
A smaller standard deviation indicates that the data is tightly clustered, while a large number indicates that the results are more spread out. The more tightly clustered, the less variability in the measurement. The standard deviation by itself does not consider the absolute value of the mean and only measures the dispersion, so it only tells us if the results are clustered, but nothing about what that cluster means in practical terms for the hobbyist.
For example, when looking at the data in Table 1 for Vendor A, let us consider chloride which has a standard deviation of 101.88 mg/L, and calcium which has a standard deviation of 7.66 mg/L. The standard deviation of the calcium measurement has a much smaller standard deviation compared to that of chloride. This might lead us to believe that the test does a worse job on repeatability of chloride measurements. However, it is interesting to also note that the mean value is 19,948.6 mg/L for chloride and 395.8 mg/L for calcium, and the ratio of the SD with respect to the mean is smaller for chloride than it is for calcium.
This ratio is called Coefficient of Variation (CV). CV is defined as the standard deviation divided by the mean and captures the variation as a function of the mean value of the measurements. The chloride has a CV of 0.51%, Calcium has a CV of 1.94%. So, while the standard deviation for Calcium is much lower than Chloride, it has a larger relative standard deviation when compared to Chloride. When evaluating measurements that are expected to be precise such as ICP, a CV value 15% may be considered acceptable [5].
This data can also be used to provide additional information, such as establishing confidence intervals on the mean value. These confidence intervals can be used to assess the amount of uncertainty in the data. The confidence interval is typically calculated using the formula shown below. For 95% confidence interval, z=1.96
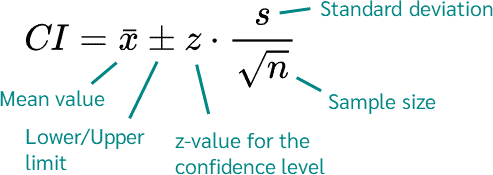
https://datatab.net/assets/tutorial/Confidence_interval_formula.png
What this tells us is that we can be 95% confident that considering the spread of the data for Vendor, the true mean lies somewhere between the upper and lower values of the 95% confidence interval (CI). In other words, if we were to perform the test 100 times on the same water sample, 95 times the results would be within the 95% confidence interval.
The margin of error is provided by
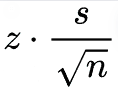
Tables 1-3 show the results from each vendor A, B, and C, along with the computed mean, standard deviation, coefficient of variation (CV as %), 95% Confidence Intervals, and the 95% confidence intervals expressed as a percentage.
Table 1: Results from Vendor A
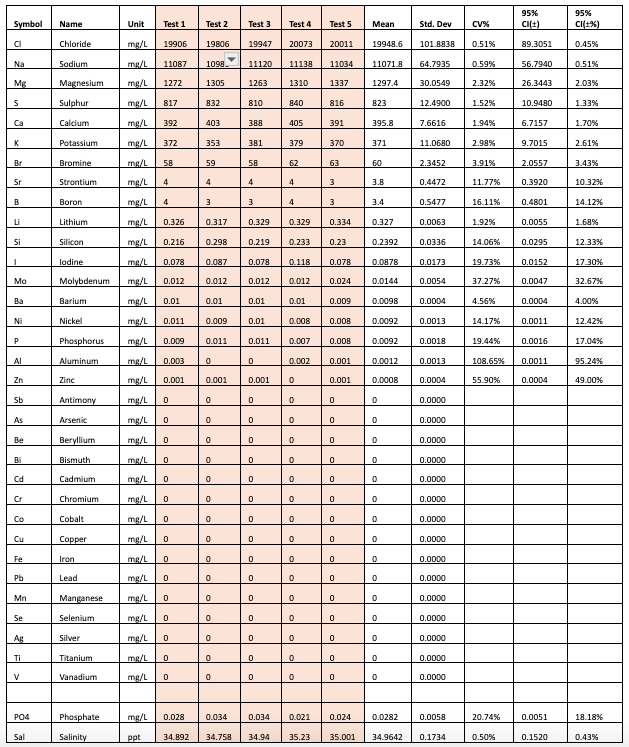
Table 2 – Results from Vendor B
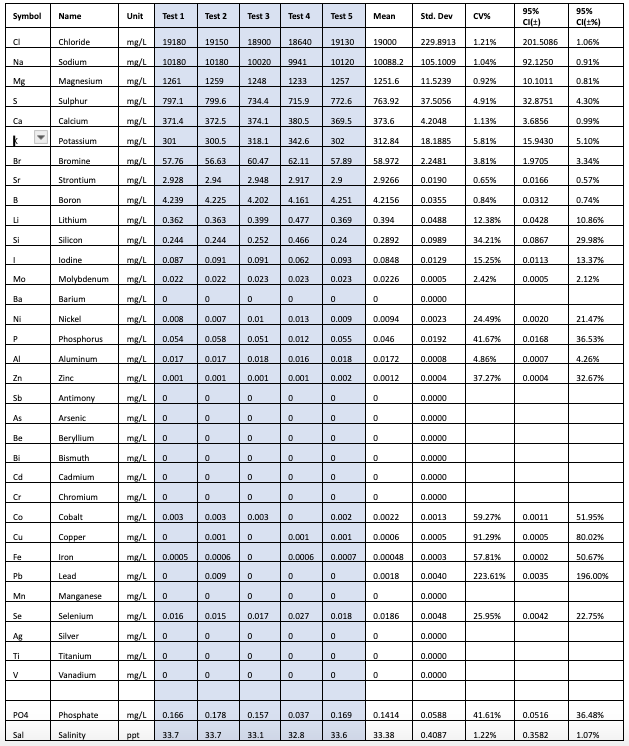
Table 3 – Results from Vendor C
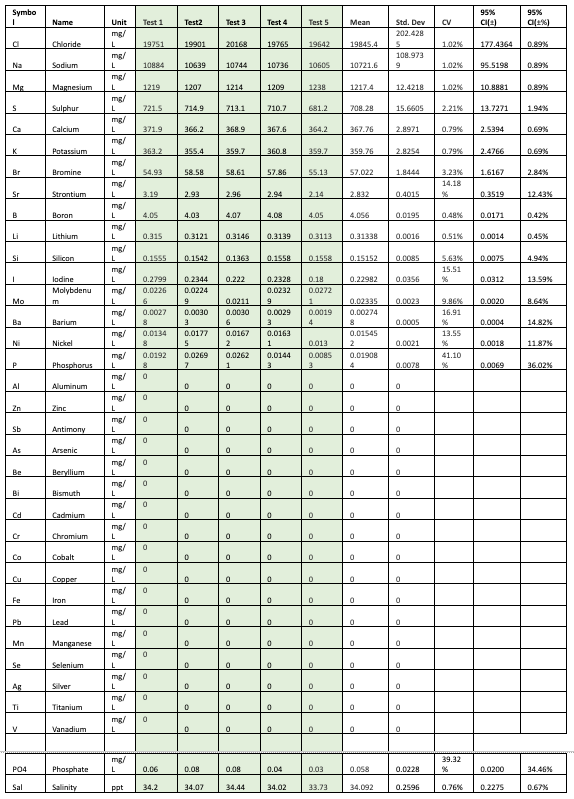
As seen from the results, the ICP tests each seem to have low CV (less than 5%) for most of the major elements. The data can also be used to make comparisons between the SD of the measurements between the vendors for each element. For example we can see that for Chloride Vendor A has a SD=101.8838, Vendor B has a SD=229.8913 and Vendor C has a SD=202.4285.
Clearly vendor A seems to have a higher repeatability on the chloride measurement. As you look at this data you will also notice that just having a higher repeatability on one element, does not imply that this will be the same case for all elements measured by Vendor A. Hence it seems that each element will have to be evaluated separately.
The data also shows that while the tests have low CV for the major elements, there is more variation in the trace elements at lower concentrations, well above the acceptable cutoff of 15%.
2. Differences between the ICP Tests
For each element in Tables 1-3, we can graphically visualize the results using plots of the data. As shown in Table 5. These graphs show the mean for each vendor (denoted by the blue dot) and the individual values (indicated by the gray dots). At this point, we can ask the question – Are the results from the three vendors different? If there are differences in the means, are these differences statistically significant enough to say that the mean values of the reported data are different given the variability in the measurements?
Table 4 – Individual value plots for each element and each Vendor
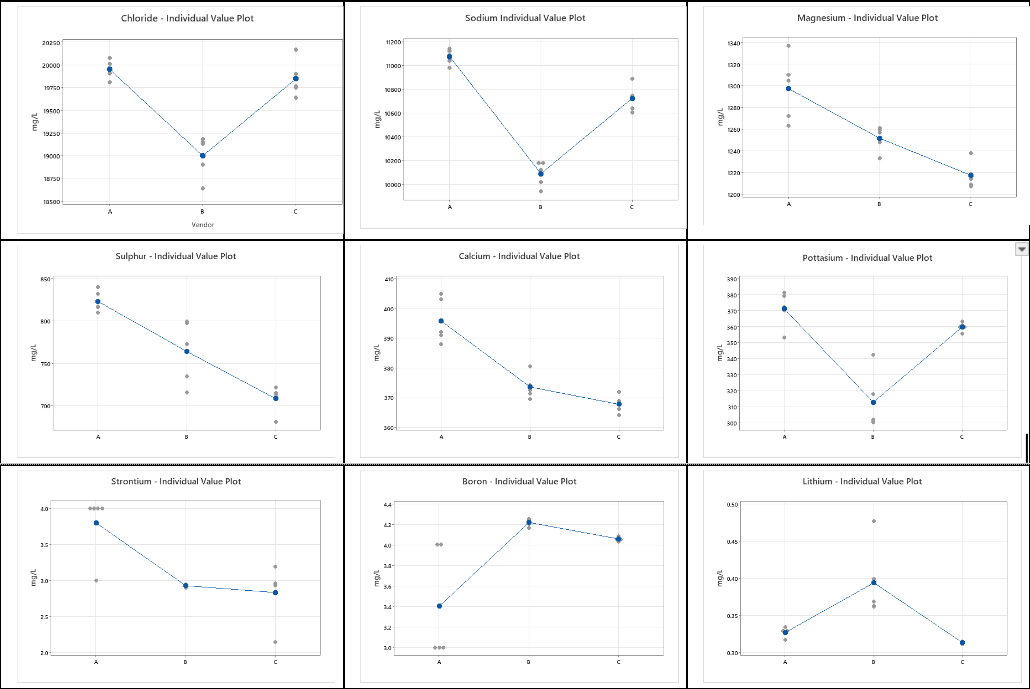
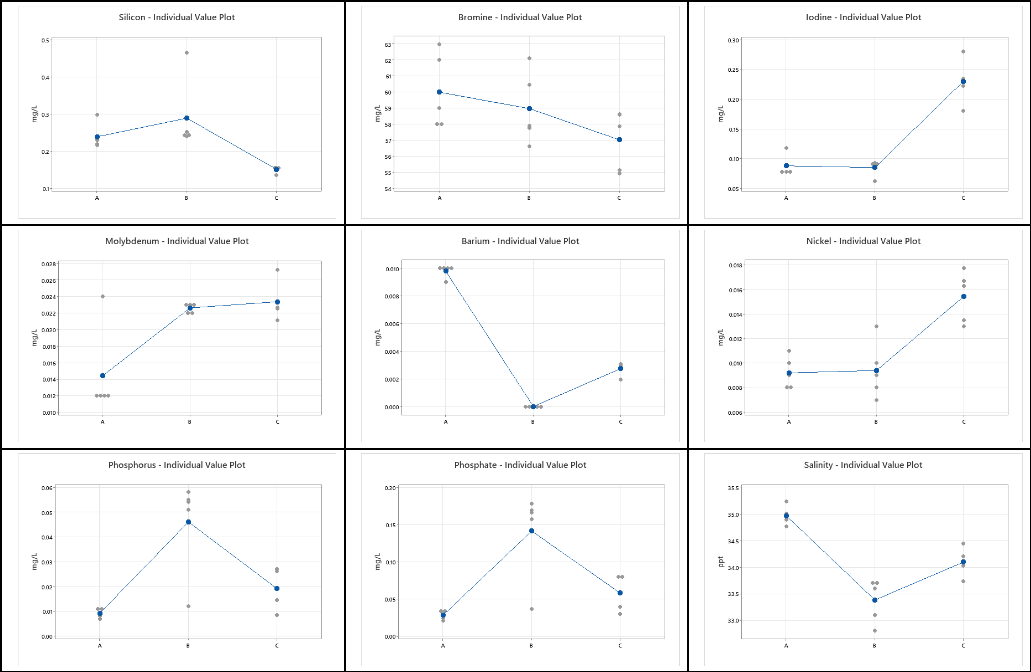
A visual inspection of the plots in Table 4 makes it quite clear that there are differences in the mean value obtained from the five results across the three different vendors. There are also differences in the standard deviation among the three vendors for each of the elements.
Instead of making these inferences visually, we rely on statistical techniques that allow us to state conclusions with a certain degree of confidence. These techniques consider the inherent variability in the measurements. Well-established statistical techniques that rely on the analysis of the variance, called ANOVA, are used to make statistically valid statements about the mean values in the presence of variability around the mean. ANOVA has been shown to be robust even in cases where the assumption that the data is from a normal distribution does not hold, and hence is acceptable for use here [6].
In our case, we are using the same water sample and are interested in knowing whether there are significant differences between the results provided for each of the elements by the 3 vendors. Here we have one factor (Vendor) that is changed across the samples, so a one-way ANOVA is used. We start with the assumption that all the tests provide results that are statistically equal. This implies that the mean values from each test are statistically identical, and the mean values from each test can essentially be considered equal.
This is the null hypothesis that is statistically tested. So, we start with the assumption that the mean values for each of the elements in the water are equal and use the statistical test to either reject this hypothesis or fail to reject this hypothesis. If we reject the hypothesis, then that implies that all the means are not equal, and there are statistically significant differences between the ICP tests when measuring the element.
There is always a probability of making the wrong conclusion, and rejecting the null hypothesis when in fact it is true. This is typically referred to as Type I error (false positive). For our analysis, we set this probability to 5% (typical value for ANOVA). This implies that we can state our conclusion about the null hypothesis with 95% confidence that we are making the correct conclusion.
Table 5 shows the result of One Factor ANOVA for each of the elements and the corresponding decision when using ? = 0.05. The results were computed using the Minitab statistical software. Elements that were not detected by one or more tests were not considered in the analysis.
Table 5 – Results of ANOVA and decision on the Null Hypothesis that All Means are Equal.
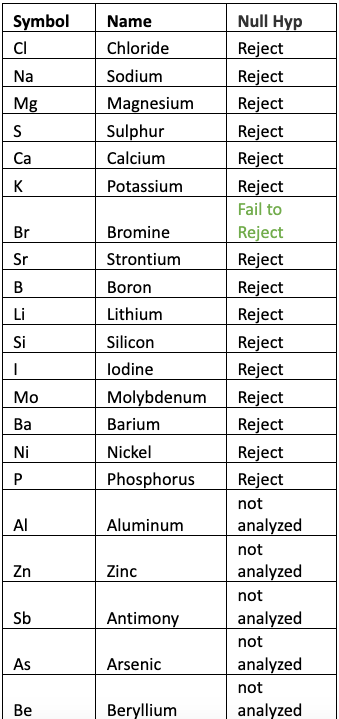
Rejecting the Null Hypothesis implies that the means are not equal, which implies that there is at least one mean that is statistically different. As seen from the table we can state with a high degree of confidence (95% confidence level) that the mean values for each element (except Bromine) analyzed are statistically NOT EQUAL.
Now that we know that the three means are not equal, hence there must be at least one mean that is statistically not equal. An additional test can be performed to determine this. The test called Tukey’s test is performed after the ANOVA. Tukey’s test compares all pairs of means and determines if the difference between them is statistically significant. Table 6 shows the result of comparing the pairs of means for each of the elements obtained by the three vendors with ? = 0.05.
Table 6: Results of Tukey’s Test to determine which pairs of means are statistically different.
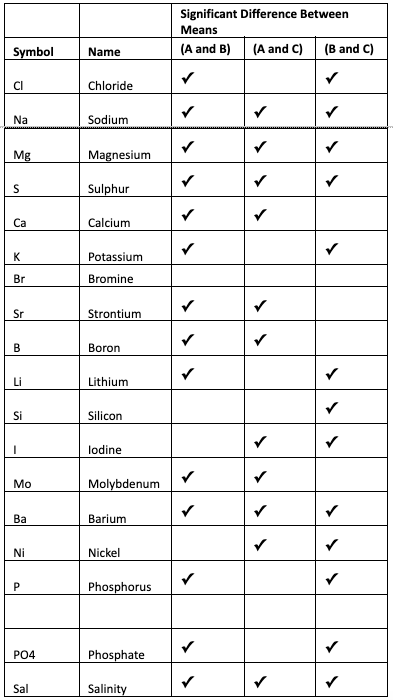
From reviewing the results in Table 6, it is obvious that there is no agreement between the ICP tests on all the elements except Bromine. On some tests there are 2 that agree and the difference between them is not significant. Using Chloride as an example, there are significant differences between the mean values reported by vendor A and B, as well as between B and C, and there is no significant difference between A and C.
Conclusions
This study demonstrates that the individual ICP tests show good repeatability within each vendor for the test results of major elements as shown by the low coefficient of variation (CV). The variability is higher for the trace elements in low concentrations.
When comparing the results across vendors it quickly becomes obvious that there are larger differences in the results across the different ICP vendors. What this analysis has shown is that these differences are statistically significant. There is no agreement across the board for all elements or even which two vendors’ overall results can be considered similar.
Part of the reason for this study was to try to get a sense of the margin of error for hobby ICP test results, as the vendors are generally unwilling to provide that information. Many home test kits provide a margin of error for the test results, so if you perform the test properly and with best practices you can have an idea about how confident you should be about your result, and if the results require action on your part.
Margin of error is usually reported as a +/- of a percentage or in the units the test kit reports. So, say a Ca test kit has a +/- of 2% – this means that your result of 440 ppm is somewhere between 431 and 449 – if you have successfully followed the instructions properly for best accuracy. Since Calcium is a major ion, there is a lot of it in saltwater, and the margin of error is less of a factor because the practical difference between 392ppm and 408ppm is unimportant to most hobbyists.
Even if the margin of error was +/-10%, (a result of 440 would be somewhere between 406 and 484) most aquarists wouldn’t worry too much about the margin of error, and take no substantial action based on the test result because we have a good understanding about how much Ca we should have in our tanks. For the minor elements, this determination is more difficult.
The data also shows that the margin of error for trace elements is higher. From Table 2, the margin of error for nickel based on the 5 test results of the same sample from a single vendor B is +/-21.46%. Since we have less of an understanding of how much nickel we should have in our tanks than we do of calcium (and this is true for most if not all the minor trace elements), determining if a test result of .0175ppm is actionable or not is difficult and subjective.
How much nickel is too much, how much is not enough, and how does a 21% margin of error impact your decision to take action? The determination around what to do with a nickel ICP result is further confusing because nickel results on reef tanks via ICP is often high compared to a recommended range (and every ICP vendor has their own set of recommended ranges), but even at those ‘elevated’ levels, many aquarists report not coral health, color, or growth issues.
According to the data, potential margins of error for each element from each vendor vary quite a bit, so as much as we would like to say the testing from any one of the three vendors comes with a margin of error of X, we cannot, and results for each element needs to be looked at individually.
ICP testing of major elements seems to have a small margin of error but has a larger margin of error for trace elements than most people seem to expect from such an instrument. Each aquarist will have to determine how much margin of error matters to them for each element in ICP results. The results between ICP companies can vary quite a bit, so if you are looking to ICP for monitoring tank chemistry over time, you may be best served by picking one company and sticking with them.
While this series of test shows what someone might expect from test results in terms of repeatability, margins of error, and confidence in the numbers, it has also shown that there is no agreement among all three with respect to the mean values obtained. It would certainly help the hobbyist if the companies provided their own assessment of the margins of error and repeatability. The question of accuracy is still unanswered and will remain so until a good seawater reference that includes all the minor trace elements can be obtained and tested across all the ICP vendors.
Acknowledgements
Special thanks to Chris Maupin, Jim Welsh, Todd Kunkel, Adam Staude, Jordan Nael, and other members of the Reef Beef community that helped make this write-up happen. Thanks to Reef Beef Podcast for funding the testing.
References
- Richard Ross and Dr. Chris Maupin, “Triton Lab ICP-OES Testing of a Certified Artificial Saltwater Standard”, https://reefs.com/magazine/skeptical-reefkeeping-12/ , 2016
- Dan, P., Taricha, and Rick Mathews, “How We Use ICP-OES Results Of Unknown Accuracy And Precision”, https://www.reef2reef.com/ams/how-we-use-icp-oes-results-of-unknown-accuracy-and-precision.862/, 2022.
- Sanjay Joshi, “The Reef Builders’ Big ICP Test Review”, https://reefbuilders.com/2023/07/12/the-reef-builders-big-icp-test-review-by-sanjay-joshi/, 2023.
- Reef Beef Podcast, https://reefbeefpodcast.com/
- Analytical method Validation: ICP-OES https://www.rsc.org/suppdata/c5/ja/c5ja00419e/c5ja00419e1.pdf
Non-normal data: Is ANOVA still a valid option?, https://www.psicothema.com/pi?pii=4434
About the authors
Sanjay Joshi is a Professor of Industrial and Manufacturing Engineering at Penn State University and has been on the reefing scene since 1992. He runs a 500-gallon tank at the university as well as a 500-gallon SPS dominant reef tank at home. He has published many articles in magazines over the years including Marine Fish and Reef Annual, Aquarium Frontiers, Aquarium Fish, and Advanced Aquarist. He has been an invited speaker at several marine aquarium society meetings in the US and Europe, including headlining our very own ReefStock. He also received the MASNA award for his contributions to the marine aquarium hobby in 2006.
Richard Ross is known for his “Skeptical Reefkeeping” article series, his one-of-a-kind presentations, his coral spawning and cephalopod research, the Reef Beef Podcast, and for managing the 212,000 gallon reef tank in the Steinhart Aquarium at the California Academy of Sciences. Through multiple different facets of aquarium research and experience, he’s created a prominent name for himself within the industry. He has kept saltwater animals and tanks for over 40 years, and has won multiple awards including the 2014 MASNA Aquarist of the Year. His work has been covered by Scientific American, National Geographic, Animal Planet, Penn’s Sunday School, NPR’s Science Friday, Discovery News, Adam Savage, Fox News, and more!


